Microwave Imaging using Neural Operators

by K. Arjun — Convolutional Neural Operator (CNO) surrogate for electromagnetic forward scattering

Introduction

Microwave imaging (MWI) uses electromagnetic waves to probe the interior of a medium via its scattered fields. Classical numerical solvers such as the Finite Difference Time Domain (FDTD), Finite Difference Frequency Domain (FDFD), and Method of Moments (MoM) provide accurate solutions to Maxwell’s equations, but are often too slow for large-scale or near real-time applications.

In this project, I approximate the forward scattering operator using a Convolutional Neural Operator (CNO). Once trained, the CNO serves as a fast surrogate that maps material permittivity and incident fields to total (or scattered) fields much faster than traditional solvers.

Forward Problem Definition

The goal is to learn a mapping from spatially varying relative permittivity $\varepsilon_r(x,y)$ and a given incident field $E_i(x,y)$ to the resulting total field $E_t(x,y)$:

$$ (E_i, \varepsilon_r) \;\longrightarrow\; E_t, \qquad E_t = E_i + E_s. $$

All fields are complex-valued:

$$ E(x,y) = \operatorname{Re}(E) + j\,\operatorname{Im}(E). $$

Helmholtz Equation for 2D TM Mode

For a 2D transverse magnetic (TM) formulation with non-zero $E_z(x,y)$ and invariance along the $z$-axis, the scalar Helmholtz equation is

$$ \nabla^2 E_z(x,y) + k^2(x,y)\,E_z(x,y) = 0, $$

where $$ k^2(x,y) = \omega^2 \mu_0 \varepsilon(x,y). $$

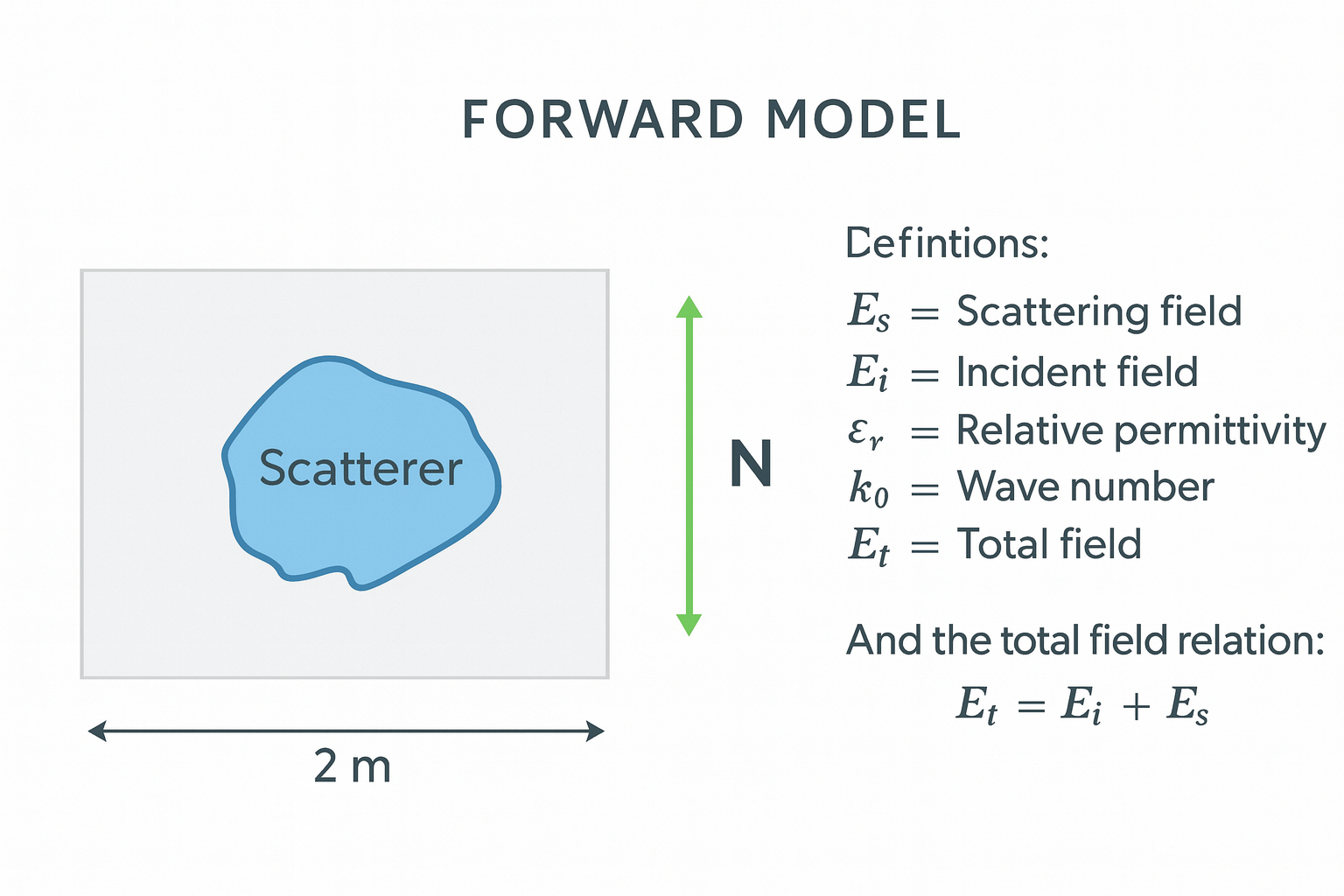
Forward electromagnetic scattering model

Simulation Setup

The training dataset is generated using a numerical solver (FDFD / related frequency-domain scheme) on a fixed 2D domain. The key parameters match the configuration used in the report:

Operating frequency: 400 MHz
Wavelength: $\lambda = 0.75\,\text{m}$
Domain size: $2\text{ m} \times 2\text{ m}$
Grid resolution: $32 \times 32$ points
Grid spacing: $h = \lambda / 12$
Relative permittivity: $\operatorname{Re}(\varepsilon_r) \in [1, 2.2]$, $\operatorname{Im}(\varepsilon_r) \in [-0.2, 0]$
Excitation: 2D TM plane wave incident on circular/inhomogeneous scatterers

Discretized computational domain and scatterers

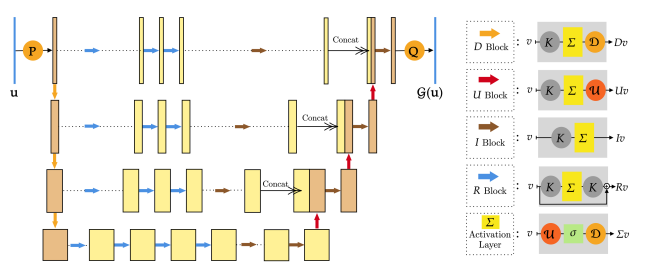
CNO Model Architecture

The model follows the Convolutional Neural Operator (CNO) architecture described in the 2023 CNO paper, adapted to complex-valued electromagnetic fields. The network operates on tensor-valued inputs defined on the grid and learns a resolution-agnostic operator in feature space.

Input channels: real/imag parts of $\varepsilon_r$, incident field, and auxiliary features
Encoder: lifts inputs to a higher-dimensional feature space
CNO blocks: local projections + convolutional mixing + residual connections
Decoder: projects features back to 2 channels (real and imaginary parts of $E_t$)
Activation: Swish
Optimizer: AdamW (learning rate $10^{-3}$, weight decay 0.001)
Batch size: 80, epochs: 100, validation split: 20%

Convolutional Neural Operator architecture used in the project

Loss and Error Metrics

Complex Mean Squared Error (MSE)

Let $z_i$ and $\hat{z}_i$ denote the ground-truth and predicted complex fields at grid point $i$. The complex MSE over a dataset of size $N$ is

$$ \text{MSE} = \frac{1}{N} \sum_{i=1}^{N} \left| \hat{z}_i - z_i \right|^2, $$

where $$ |z|^2 = (\Re(z))^2 + (\Im(z))^2. $$

Complex Relative Error

The complex relative error is

$$ \text{RelErr} = \frac{1}{N} \sum_{i=1}^{N} \frac{ \left| \hat{z}_i - z_i \right| }{ \left| z_i \right| }. $$

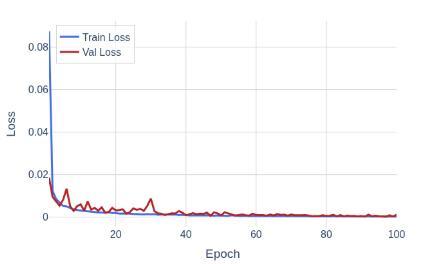
Training Loss vs Epoch

Training and validation curves for the complex MSE show stable convergence without severe overfitting.

Training and validation loss versus epoch

Qualitative Results

The figures below show visual comparisons between numerical solver output and CNO predictions for representative samples.

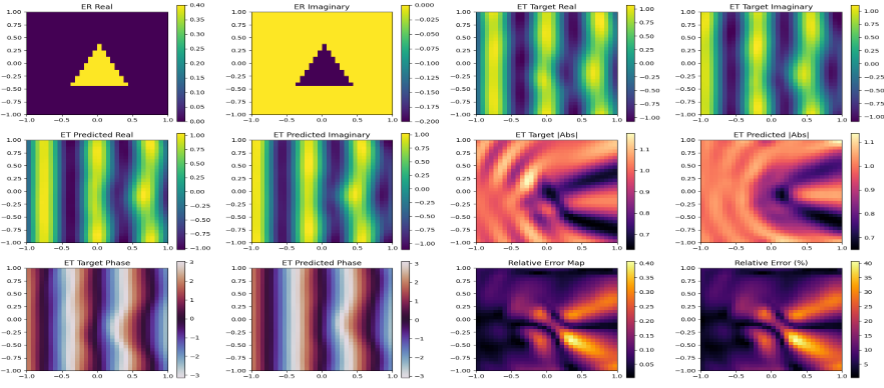
Training Samples

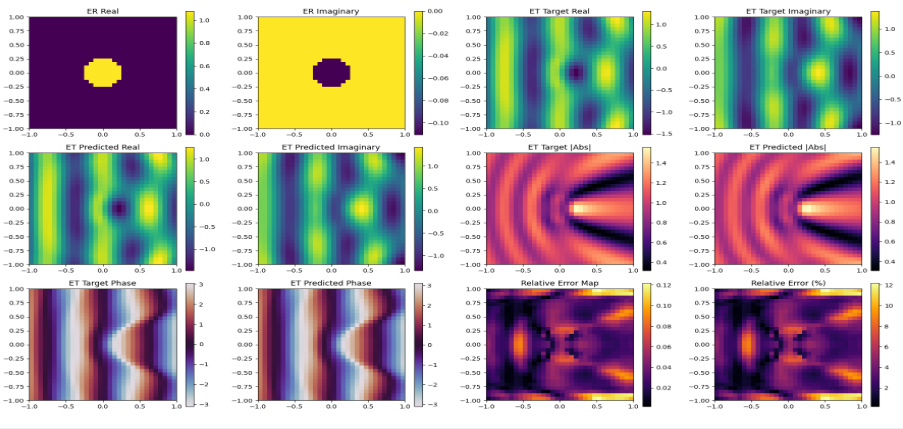
Representative training-set samples: ground truth vs CNO prediction

In-Distribution Validation (ID)

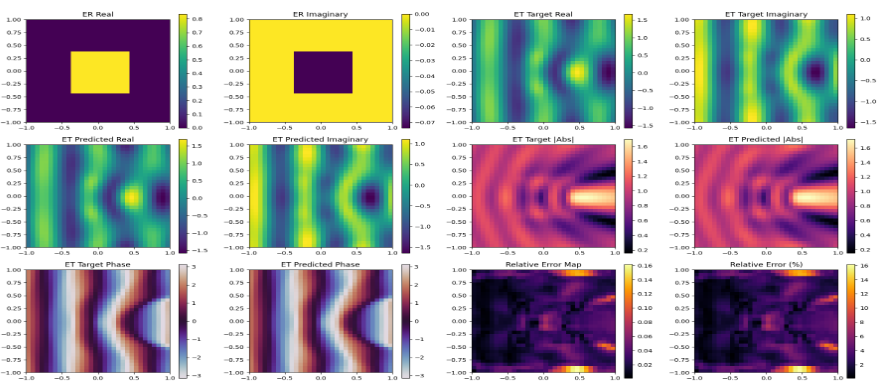
In-distribution validation samples: ground truth vs CNO prediction

Out-of-Distribution (OOD) Test

Out-of-distribution test samples: generalization of the CNO model

Quantitative Performance

Performance is reported separately for in-distribution (ID) and out-of-distribution (OOD) configurations:

In-distribution (ID): typical complex relative error

$\text{RelErr}_{\text{ID}} \approx 2\% \text{–} 3\%$

Out-of-distribution (OOD): for unseen shapes and permittivity ranges

$\text{RelErr}_{\text{OOD}} \approx 9\% \text{–} 12\%$

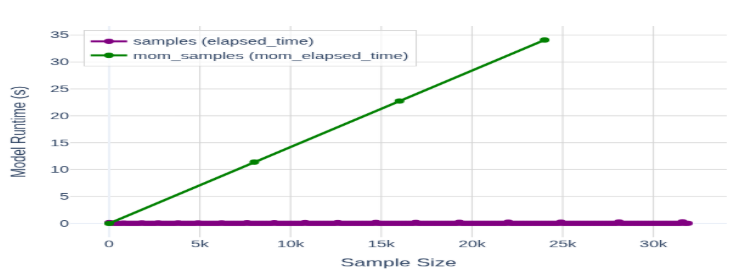
Runtime Comparison

One of the main advantages of a neural-operator surrogate is its fast inference time compared to classical solvers.

CNO inference time: $\approx 0.05$ seconds per sample (on a GPU setup)
FDFD / MoM: typically seconds to minutes per sample for comparable resolution

Runtime comparison between CNO and traditional EM solvers

Tools and Implementation

Language: Python
Core library: JAX
Neural network library: FLAX / NNX
Training: custom CNO implementation with AdamW optimization

Source Code

Full training and evaluation code is available at GitHub repository .

Project Report

This work is based on my B.Tech project report . “Microwave Imaging using Neural Operators” completed at IIITDM Kurnool, under the supervision of Dr. Yashwanth Kalepu .